目录
快速导航-

艺术视角 | 升清质之悠悠,降澄辉之蔼蔼
艺术视角 | 升清质之悠悠,降澄辉之蔼蔼
-
“图形的性质”专题复习 | 深谙几何特征,方知图形性质
“图形的性质”专题复习 | 深谙几何特征,方知图形性质
-
“图形的性质”专题复习 | 掌握图形性质 构建知识体系
“图形的性质”专题复习 | 掌握图形性质 构建知识体系
-
“图形的性质”专题复习 | 理解图形性质 厘清推理依据
“图形的性质”专题复习 | 理解图形性质 厘清推理依据
-
“图形的性质”专题复习 | 理解本质 明晰错因
“图形的性质”专题复习 | 理解本质 明晰错因
-
“图形的性质”专题复习 | 深挖教材习题,把握中考考点
“图形的性质”专题复习 | 深挖教材习题,把握中考考点
-
“图形的性质”专题复习 | 四边形的中考之旅
“图形的性质”专题复习 | 四边形的中考之旅
-
“图形的性质”专题复习 | 数学眼光看世界 发挥想象找关系
“图形的性质”专题复习 | 数学眼光看世界 发挥想象找关系
-
“图形的变化”专题复习 | 整体中思考 变化中做题
“图形的变化”专题复习 | 整体中思考 变化中做题
-
“图形的变化”专题复习 | 辩证思考“动”与“静”,感受“图形变化”
“图形的变化”专题复习 | 辩证思考“动”与“静”,感受“图形变化”
-
“图形的变化”专题复习 | 心中明确关键步 精准踩中得分点
“图形的变化”专题复习 | 心中明确关键步 精准踩中得分点
-
“图形的变化”专题复习 | 以动制静,方能化难为易
“图形的变化”专题复习 | 以动制静,方能化难为易
-
“图形的变化”专题复习 | “图”个明白,成功绕“坑”
“图形的变化”专题复习 | “图”个明白,成功绕“坑”
-
“图形的变化”专题复习 | 动静结合应对图形之“变”
“图形的变化”专题复习 | 动静结合应对图形之“变”
-
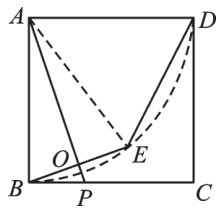
“图形的变化”专题复习 | 破解图形变化迷局
“图形的变化”专题复习 | 破解图形变化迷局
-
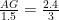
“图形的变化”专题复习 | 在变化中探索几何的韵味
“图形的变化”专题复习 | 在变化中探索几何的韵味
-
“图形与坐标”专题复习 | 图形与坐标 数学好搭档
“图形与坐标”专题复习 | 图形与坐标 数学好搭档
-
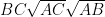
“图形与坐标”专题复习 | 精细阅读 精准答题
“图形与坐标”专题复习 | 精细阅读 精准答题
-
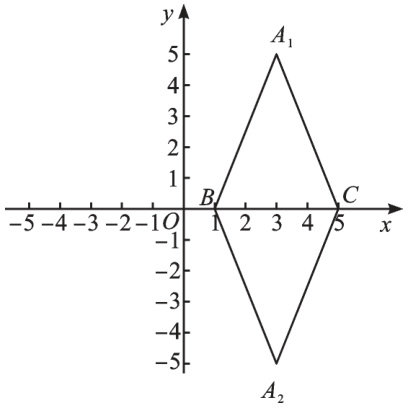
“图形与坐标”专题复习 | 对一道教材例题的变式与思考
“图形与坐标”专题复习 | 对一道教材例题的变式与思考
-
“图形与坐标”专题复习 | “数形结合”巧解动点问题
“图形与坐标”专题复习 | “数形结合”巧解动点问题
-
“图形与坐标”专题复习 | 依据图形特征,遨游坐标世界
“图形与坐标”专题复习 | 依据图形特征,遨游坐标世界
-
“图形与坐标”专题复习 | 藏宝地之谜
“图形与坐标”专题复习 | 藏宝地之谜
-

备考指导 | 找出问题本质,提升审题能力
备考指导 | 找出问题本质,提升审题能力
-
备考指导 | 选择题解答策略
备考指导 | 选择题解答策略
-
备考指导 | 填空题解答策略
备考指导 | 填空题解答策略
-
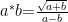
备考指导 | 新定义型问题解答策略
备考指导 | 新定义型问题解答策略
-
备考指导 | 尺规作图题解答策略
备考指导 | 尺规作图题解答策略
-
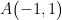
备考指导 | 几何直观题解答策略
备考指导 | 几何直观题解答策略
-
备考指导 | 代数推理题解答策略
备考指导 | 代数推理题解答策略
-
备考指导 | 跨学科问题解答策略
备考指导 | 跨学科问题解答策略
-
备考指导 | 综合与实践题解答策略
备考指导 | 综合与实践题解答策略























 登录
登录